“One Guinness, be sure to!” says a shopper to a barkeep, who flips a branded pint glass and catches it underneath the faucet. The barkeep starts a multistep pour system long lasting exactly 119.5 seconds, which, no matter whether it is a promoting gimmick or a marvel of alcoholic engineering, has grow to be a beloved ritual in Irish pubs globally. The consequence: a loaded stout with a best froth layer like an earthy milkshake.
The Guinness brewery has been acknowledged for ground breaking solutions ever because founder Arthur Guinness signed a 9,000-year lease in Dublin for £45 a calendar year. For case in point, a mathematician-turned-brewer invented a chemical procedure there just after four many years of tinkering that presents the brewery’s namesake stout its velvety head. The approach, which involves including nitrogen fuel to kegs and to little balls inside cans of Guinness, led to today’s vastly popular “nitro” brews for beer and coffee.
But the most influential innovation to arrive out of the brewery by considerably has almost nothing to do with beer. It was the birthplace of the t-examination, a person of the most significant statistical strategies in all of science. When experts declare their results “statistically important,” they pretty normally use a t-exam to make that resolve. How does this function, and why did it originate in beer brewing, of all places?
On supporting science journalism
If you are making the most of this post, look at supporting our award-successful journalism by subscribing. By getting a membership you are aiding to guarantee the potential of impactful stories about the discoveries and suggestions shaping our earth now.
Close to the start of the 20th century, Guinness experienced been in operation for virtually 150 a long time and towered in excess of its competitors as the world’s most significant brewery. Right up until then, excellent command on its solutions consisted of tough eyeballing and smell tests. But the calls for of international growth inspired Guinness leaders to revamp their technique to goal consistency and industrial-grade rigor. The business hired a workforce of brainiacs and gave them latitude to go after study inquiries in service of the fantastic brew. The brewery grew to become a hub of experimentation to reply an array of inquiries: Exactly where do the very best barley kinds develop? What is the best saccharine level in malt extract? How significantly did the newest ad campaign boost profits?
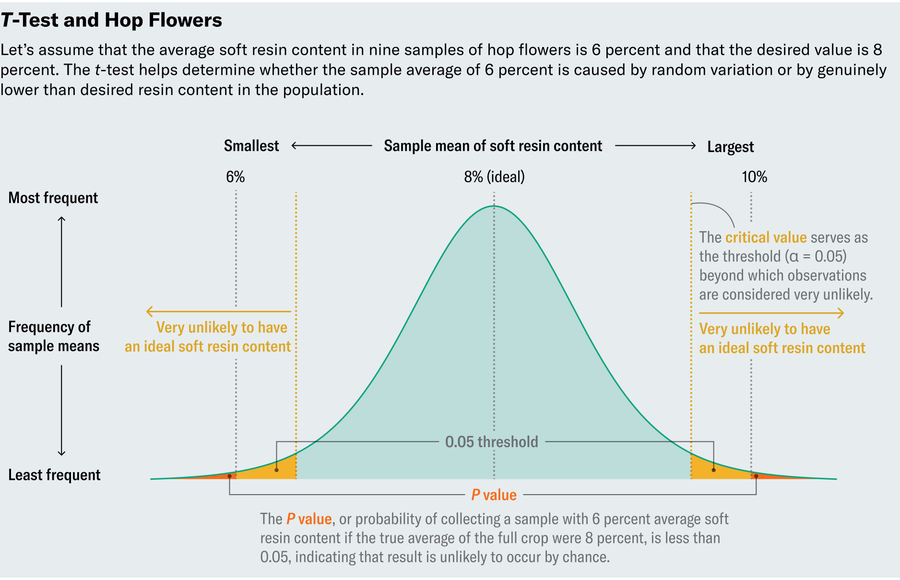
Amid the flurry of scientific energy, the team faced a persistent issue: deciphering its data in the experience of modest sample dimensions. One particular problem the brewers confronted will involve hop bouquets, essential substances in Guinness that impart a bitter flavor and act as a normal preservative. To assess the excellent of hops, brewers calculated the comfortable resin content in the plants. Let us say they deemed 8 p.c a very good and regular value. Tests each and every flower in the crop wasn’t economically practical, nevertheless. So they did what any excellent scientist would do and tested random samples of bouquets.
Let’s inspect a manufactured-up instance. Suppose we measure delicate resin material in nine samples and, simply because samples range, notice a selection of values from 4 percent to 10 per cent, with an ordinary of 6 percent—too very low. Does that imply we should dump the crop? Uncertainty creeps in from two probable explanations for the low measurements. Possibly the crop actually does comprise unusually small tender resin written content, or nevertheless the samples incorporate lower amounts, the whole crop is in fact fine. The whole place of having random samples is to count on them as faithful reps of the total crop, but potentially we ended up unfortunate by picking samples with uncharacteristically low amounts. (We only tested 9, immediately after all.) In other terms, should we think about the small stages in our samples drastically different from 8 percent or mere natural variation?
This quandary is not exceptional to brewing. Somewhat, it pervades all scientific inquiry. Suppose that in a professional medical trial, both the treatment method group and placebo team increase, but the procedure group fares a tiny better. Does that present ample grounds to advise the medicine? What if I informed you that both of those teams truly obtained two unique placebos? Would you be tempted to conclude that the placebo in the group with better outcomes ought to have medicinal homes? Or could it be that when you keep track of a team of people today, some of them will just by natural means strengthen, at times by a minimal and often by a ton? Yet again, this boils down to a question of statistical significance.
The principle underlying these perennial queries in the area of tiny sample sizes hadn’t been developed until eventually Guinness came on the scene—specifically, not right up until William Sealy Gosset, head experimental brewer at Guinness in the early 20th century, invented the t-check. The concept of statistical importance predated Gosset, but prior statisticians worked in the regime of massive sample sizes. To value why this difference matters, we require to realize how a single would figure out statistical importance.
Don’t forget, the hops samples in our situation have an common gentle resin information of 6 percent, and we want to know regardless of whether the normal in the entire crop basically differs from the sought after 8 per cent or if we just received unlucky with our sample. So we’ll ask the query: What is the probability that we would observe such an extreme benefit (6 %) if the comprehensive crop was in fact common (with an common of 8 %)?Typically, if this probability, termed a P worth, lies beneath .05, then we deem the deviation statistically major, although diverse programs contact for unique thresholds.
Often two independent aspects impact the P benefit: how much a sample deviates from what is predicted in a inhabitants and how frequent large deviations are. Think of this as a tug-of-war concerning signal and sound. The big difference between our observed indicate (6 %) and our sought after one particular (8 p.c) delivers the signal—the much larger this variation, the a lot more very likely the crop seriously does have lower comfortable resin content material. The typical deviation between bouquets provides the noise. Conventional deviation actions how spread out the knowledge are all around the indicate compact values point out that the data hover around the suggest, and larger sized values suggest broader variation. If the gentle resin material normally fluctuates commonly throughout buds (in other words, has a substantial conventional deviation), then perhaps the 6 p.c ordinary in our sample shouldn’t worry us. But if bouquets are inclined to exhibit regularity (or a small conventional deviation), then 6 % might suggest a accurate deviation from the sought after 8 percent.
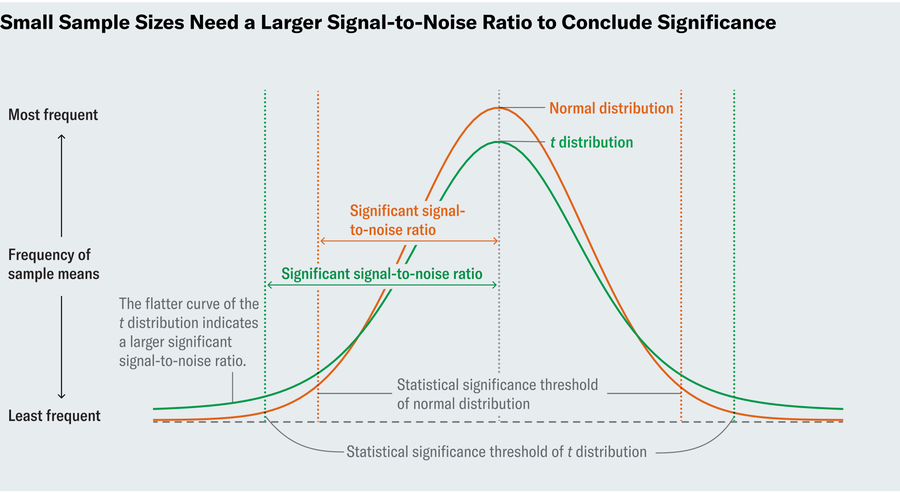
To decide a P price in an great earth, we’d commence by calculating the sign-to-sounds ratio. The better this ratio, the much more assurance we have in the significance of our conclusions mainly because a superior ratio suggests that we have discovered a correct deviation. But what counts as superior signal-to-noise? To deem 6 % drastically diverse from 8 %, we specially want to know when the signal-to-sounds ratio is so high that it only has a 5 percent chance of transpiring in a earth where an 8 per cent resin written content is the norm. Statisticians in Gosset’s time knew that if you were being to operate an experiment quite a few occasions, determine the sign-to-sound ratio in each and every of individuals experiments and graph the final results, that plot would resemble a “standard normal distribution”—the familiar bell curve. Mainly because the standard distribution is perfectly understood and documented, you can search up in a table how huge the ratio need to be to achieve the 5 % threshold (or any other threshold).
Gosset regarded that this solution only worked with large sample measurements, whereas tiny samples of hops would not guarantee that ordinary distribution. So he meticulously tabulated new distributions for scaled-down sample dimensions. Now regarded as t-distributions, these plots resemble the normal distribution in that they’re bell-formed, but the curves of the bell do not drop off as sharply. That interprets to needing an even much larger signal-to-sound ratio to conclude importance. His t-check will allow us to make inferences in options the place we could not just before.
Mathematical specialist John D. Cook mused on his website in 2008 that perhaps it should really not surprise us that the t-exam originated at a brewery as opposed to, say, a winery. Brewers desire consistency in their merchandise, whilst vintners revel in range. Wines have “good many years,” and each and every bottle tells a tale, but you want each individual pour of Guinness to supply the similar trademark style. In this case, uniformity impressed innovation.
Gosset solved quite a few issues at the brewery with his new method. The self-taught statistician printed his t-take a look at below the pseudonym “Student” because Guinness did not want to tip off opponents to its analysis. Though Gosset pioneered industrial quality management and contributed masses of other thoughts to quantitative study, most textbooks still phone his fantastic achievement the “Student’s t-test.” Historical past could have neglected his title, but he could be happy that the t-take a look at is a person of the most greatly made use of statistical tools in science to this day. Maybe his accomplishment belongs in Guinness World Information (the thought for which was dreamed up by Guinness’s controlling director in the 1950s). Cheers to that.










:quality(85):upscale()/2024/04/11/933/n/1922441/9ec36f98661855259f3a63.35972314_.jpg)